
(이미지출처 : GIB)
수학 문제를 풀다가 막혀서 해답을 본 적이 있나요? 대부분 풀이를 보고 나면 “에이~ 뭐야, 이렇게 하면 되는 거였네?”라며 사실은 아는 내용인데, 실수로 풀지 못했다고 여깁니다. 하지만 막상 시험에 비슷한 문제가 나오면 어렴풋이 풀었던 기억만 날 뿐 맞히지 못합니다. 혹시 내 이야기인가 싶은 친구들은 오늘 주제가 솔깃할 텐데요, 오늘은 수학 해답지를 활용해 기억력의 한계를 극복하고 문제해결력까지 높이는 방법을 소개하겠습니다.
문제를 제대로 파악하지 않은 채, 해답을 보고 문제를 이해한 뒤 공부가 끝났다고 착각하는 공부 방법으로는 10시간을 공부해도 머릿속에 남는 게 없습니다. 진정한 사고를 하지 않았기 때문에 기억에 남지 않는 것이죠. 그러나 어쩔 수 없이 해답을 봐야 할 때도 있습니다. 여러 번 고민했는데도 문제가 해결되지 않을 땐 해답지를 좋은 선생님으로 활용할 수 있거든요.
독이 될 수도, 선생님이 될 수도 있는 ‘해답지’
소크라테스는 ‘문답법’으로 제자들을 가르쳤습니다. 제자에게 적절한 질문을 해 모르는 것이 무엇인지 깨닫게 하고 진리를 탐구하게 만드는 문답법은 수학 학습에 있어서 매우 유용한 도구입니다. 해답을 어떻게 활용하면 문답법과 같은 효과를 볼 수 있을까요? 비법은 해답을 보되 천천히, 그리고 거꾸로 보는 것입니다.
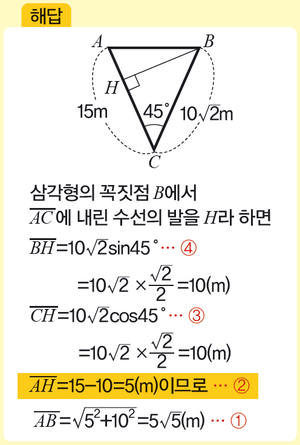
이제 위쪽의 해답을 같이 볼까요? 해답을 거꾸로 보는 게 핵심입니다. 정답 ①의 바로 윗줄 ②를 보고 멈춘 뒤 문제를 풀기 위한 힌트가 무엇인지 생각합니다. 변 AB의 길이를 구하기 위해서는 변 AH의 길이가 필요하다는 사실을 알아내는 거죠. 힌트를 알아냈으면 해답을 덮고 변 AH의 길이를 알아내는 것에 집중합니다. 문제 속의 문제를 해결하는 셈인데, 만약 이것도 해결하기 어렵다면 ③의 변 CH에만 집중합니다. 이런 식으로 ②→③→④의 순서로 한 단계씩 보면서 문제를 해결하기 위해 어떤 정보가 필요한지를 찾아냅니다.
천천히, 거꾸로 보며 결정적 한 방 찾는 연습
정답의 바로 전 단계는 문제를 해결하기 위한 결정적인 힌트인 경우가 많습니다. 그 힌트를 붙잡고 정답에 이르기 위한 필수적인 요소가 ‘바로 이것’이라는 것을 느끼는 것이 중요합니다. 이렇게 거꾸로 해답을 읽다 보면 정답에 이르기 위한 조건을 하나씩 알아낼 수 있습니다. 결정적인 한 방이 되는 셈인데, 이걸 빨리 알아내는 연습은 다음과 같은 방법으로 할 수 있습니다.
소크라테스가 제자에게 끊임없는 질문을 해 진리를 깨닫게 했듯 우리는 혼자서 해답을 활용해 나에게 질문을 할 수 있습니다. 이 질문은 정답에 이르기 위해 내가 구해야 하는 것이 무엇인지 깨닫게 해줍니다. 나아가 그것을 알아내기 위해 나는 어떤 것을 더 공부해야 하는지도 알 수 있게 하지요.
수학 공부를 하면서 계속 자신에게 질문을 던지는 것은 아주 좋은 학습법입니다. 질문에 답을 할 수 있다는 것은 정확히 알고 있을 때만 가능하고 반대로 답을 할 수 없다는 것은 어딘가 부족하다는 의미니까요. 우리는 스스로 소크라테스가 돼 좋은 질문에 답하며 성장할 수 있습니다. 어떤가요? 지금 당장 소크라테스를 내 책상으로 모시고 싶지 않나요?
<출처 : 수학동아 9월호>
※ 필자소개 | 오선영 교사는 20년 차 수학 교사이자 고등학생 자녀를 둔 학부모로, 현재 파주 율곡중학교에서 학생을 가르치고 있다. 블로그 ‘자기주도력발전소(blog.naver.com/sunyoh)’를 운영하며, 중학생의 수학 학습법과 고등학교 진학에 대한 콘텐츠를 꾸준히 올리고 있다.

